reveal.js

The Machine Learning Pipeline

Dr. David Elliott

Machine Learning in Python

https://bit.ly/mlped21

Orange: Preparation
Blue: Pipeline Development
Red: Decision
Green: Pipeline Evaluation
Yellow: Deployment

"Model training is only a small piece of the machine learning process."¹
"...creating successful machine learning systems involves a lot more than choosing between a random forest model and a support vector machine model."¹
"From choosing the proper ingestion mechanism to data cleansing to feature engineering, the initial steps in a machine learning pipeline are just as important as model selection. Also being able to properly measure and monitor the performance of your model in production and deciding when and how to retrain your models can be the difference between great results and mediocre outcomes. As the world changes, your input variables change, and your model must change with them."¹
"One important item to consider is that each step in the pipeline produces an output that becomes the input for the next step in the pipeline. The term pipeline is somewhat misleading as it implies a one-way flow of data. In reality, machine learning pipelines can be cyclical and iterative. Every step in the pipeline might be repeated to achieve better results or cleaner data. Finally, the output variable might be used as input the next time the pipeline cycle is performed."¹

Problem Definition

Asking and framing the right question is really important^1,2.

What are the current solutions (baseline model)?
How should performance be measured so it aligns with research/buisness objectives?
What are the minimal performance thresholds we are aiming to achieve?
Is human expertise available to help the project?

Data Collection

Obtaining relevant datasets to answer a problem might be quite difficult (e.g. expensive, time-consuming).

Data often comes from the "real world", which means it is full of human errors and biases.

You may need to consider how to source, ingest, and store data*.

*But we're not going to worry about this too much on this course.

Deciding on variables which should be part of the input data requires human (not artificial) intelligence.

Restaurant Daily Sales	Stock prices
Previous day's sales	Previous day's price
Day of the week	Interest rates
Holiday or not holiday	Company earnings
Rain or no rain	News headlines

Exploratory Data Analysis

Before applying any machine learning methods, we should explore our data.

Visualize the data,
Check model assumptions,
Look for correlations,
Identify outliers, patterns and trends.

Pre-processing

Typically data is messy and needs to be prepared for downstream transformations and modelling.

Data separation (training, validation, test sets),
Impute/remove missing values,
Correct for inconsistent values,
Remove duplicate records.

We will be focusing on this in weeks 1 and 2.
"You can then train the model on the training data in order to later make predictions on the test data. The training set is visible to the model and it is trained on this data. The training creates an inference engine that can be later applied to new data points that the model has not previously seen. The test dataset (or subset) represents this unseen data and it now can be used to make predictions on this previously unseen data."¹
Most ML models cannot handle missing values. There are a number of ways we can deal with mising values including imputing a value (e.g. mean, median) or removing observations with missing values entirely.
Data may be formatted inconsistently, for example there may be multiple ways dates are formated (e.g. 11/1/2021, 11/01/21).
We want to remove duplicates as they may bias our fitted model. In other words, we may potentially overfit to this subset of points.
Feature scaling is important as many machine learning algorithms are sensitive to the scale and magnitude of the features. Feature scaling will typically improve performance and training times. An example is to "standardise" features by centering the variable at zero and standardizing the variance to 1.

Feature Engineering

"A feature is a numeric representation of an aspect of raw data."³

Changing the distribution of your data (e.g., log transformation, standardization, min-max scaling etc.).
Higher-dimensional feature spaces (e.g., polynomials).
Lower dimensional feature spaces (dimensionality reduction, hashing, clustering).

We will be focusing on this in week 2.
Feature engineering means formulating appropriate features given the data, the model, and the task.
"There are many ways to turn raw data into numeric measurements, which is why features can end up looking like a lot of things. Naturally, features must derive from the type of data that is available. Perhaps less obvious is the fact that they are also tied to the model; some models are more appropriate for some types of features, and vice versa. The right features are relevant to the task at hand and should be easy for the model to ingest."³
"I see [feature engineering] more as a 'data/feature creation' step rather than a data 'sanitizing' step."⁴
Feature scaling is important as many machine learning algorithms are sensitive to the scale and magnitude of the features. Feature scaling will typically improve performance and training times. An example is to "standardise" features by centering the variable at zero and standardizing the variance to 1.

Dimension Reduction

We want to remove "uninformative information" and retain useful bits³.

Dimension Reduction

We want to remove "uninformative information" and retain useful bits³.

Feature Selection

Feature Extraction

Dimension Reduction

Feature Selection

Create a subset of the original set of features.

Feature Importances

Regularization

Dimension Reduction

Feature Extraction

Create new synthetic features through combining the original features and discarding less important ones.

Principal Component Analysis

Model Training

Why are there so many models?

...or put another way: Why not just learn the latest "best" model. For example, why not just focus on deep learning?

The No Free Lunch Theorem

This theoretical finding suggests all optimization algorithms perform equally well when their performance is averaged over all possible objective functions.

"In a famous 1996 paper, 11 David Wolpert demonstrated that if you make absolutely no assumption about the data, then there is no reason to prefer one model over any other. This is called the No Free Lunch (NFL) theorem. For some datasets the best model is a linear model, while for other datasets it is a neural network. There is no model that is a priori guaranteed to work better (hence the name of the theorem). The only way to know for sure which model is best is to evaluate them all. Since this is not possible, in practice you make some reasonable assumptions about the data and you evaluate only a few reasonable models. For example, for simple tasks you may evaluate linear models with various levels of regularization, and for a complex problem you may evaluate various neural networks."²
"As a consequence of the no free lunch theorem, we need to develop many different types of models, to cover the wide variety of data that occurs in the real world. And for each model, there may be many different algorithms we can use to train the model, which make different speed-accuracy-complexity tradeoffs."⁹

Interpretability vs. Accuracy

"Classical" Methods

Classical methods are categorised typically in relation to ensemble or neural network/deep learning models.

Have a background in statistics, rather than computing.
Used to find similarities in data points and searching for patterns.

Unsupervised Learning

In unsupervised learning we aim to use data: $$D = \{\mathbf{x}_n\}^N_{n=1},$$ with inputs $\mathbf{x}_n$ and $N$ training examples, to learn how to represent or find interesting patterns in the data.

$\mathbf{x}$ is a $D$-dimensional vector of numbers (e.g. a patient's blood pressure, heart rate, and weight).

These are referred to as features, covariates, attributes, or predictors.
They can also be more general objects: image, sentence/tweet, email, time series, graph, etc.

fixed acidity	volatile acidity	citric acid	residual sugar	chlorides	free sulfur dioxide	total sulfur dioxide	density	pH	sulphates	alcohol	quality
7.4	0.7	0	1.9	0.076	11	34	0.9978	3.51	0.56	9.4	5
7.8	0.88	0	2.6	0.098	25	67	0.9968	3.2	0.68	9.8	5
7.8	0.76	0.04	2.3	0.092	15	54	0.997	3.26	0.65	9.8	5
11.2	0.28	0.56	1.9	0.075	17	60	0.998	3.16	0.58	9.8	6
7.4	0.7	0	1.9	0.076	11	34	0.9978	3.51	0.56	9.4	5

For example, in clustering, we assume there are latent classes or clusters of the training data with similar behavior.

We aim to determine...

...the number of clusters.
...the cluster labels.

Example Models

K-Means
DBScan

Supervised Learning

In supervised learning, we have a training dataset of labelled input-output pairs, denoted $$D = \{(\mathbf{x}_n, y_n)\}^N_{n=1},$$ with inputs $\mathbf{x}_n$ and outputs $y_n$.

We aim to use $D$ to learn the mapping from $\mathbf{x}$ to $y$ for generalization, i.e. to automatically label future inputs $\mathbf{x}^*$.

Regression aims to learn the mapping from the inputs $\mathbf{x}$ to a continuous output $y \in \mathbb{R}$.

Example Models

Linear Regression
Ridge/Lasso Regression
Regression Tree

Classification aims to learn the mapping from the inputs $\mathbf{x}$ to a categorical output $y \in \lbrace 1, \ldots, C \rbrace$, and is known as:

binary classification when $C=2$,
multiclass classification when $C>2$,
multi-label classification when the output is a vector of non mutually exclusive labels.

Example Models

K-Nearest Neighbours
Logisitic Regression
Support Vector Machines

Bias–Variance tradeoff

bias low, variance low

Bias–Variance tradeoff

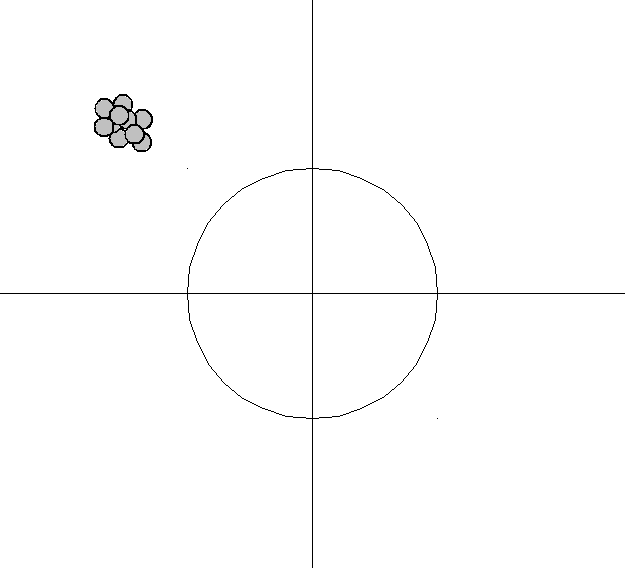
bias high, variance low

Bias–Variance tradeoff

bias low, variance high

Bias–Variance tradeoff

bias high, variance high

Ensemble Methods

Ensemble methods aim to improve generalisability of an algorithm by combining the predictions of several estimators⁵.

To achieve this there are three general methods:

Averaging
Boosting
Deep Learning

Averaging

Averaging methods build several separate estimators and then average their predictions.

For example, a bagging method averages an ensemble of base classifiers fit on random subsets of a dataset (observations and/or features) with replacement⁶.

Example Models

Random Forest
Majority Voting Classifier

Boosting

Boosting typically use an ensemble of weak estimators that are built sequentially, with each estimator attempting to reduce the bias of the predecessor².

Example Models

AdaBoost
XGBoost
CatBoost

Deep Learning

Layers of interconnected artificial neurons or other formulas are stacked on top of each other.

Example Models

Multi-layer Perceptron
Convolutional Neural Network
Recurrent Neural Network
Autoencoder

Model Evaluation & Tuning

Regression and classification use different metrics to assess the performance of a model.

Classification	Regression
Accuracy	Mean squared error
Sensitivity	Mean absolute error
Specificity	Median absolute error
Precision	$R^2$ (coefficient of determination)

We can assess how a model performs on data it is trained on (training set) and data it has not seen before (validation/test set).

While tuning our model, we could evaluate our model performance on multiple splits (e.g. K-fold cross-validation).

Model Tuning

Most models have settings we can change (hyper-parameters). Also, it may not be clear what feature pre-processing or engineering steps work best.

We could fiddle with them manually until we find a great combination (tedious)...

... or get the computer to do this for you (e.g. grid-search, random search).

Model Deployment & Monitoring

Once a model is chosen, we can deploy it into production for inference.

The model needs to be continuously monitored for model performance, retrained, and recalibrated accordingly.

References

Alberto, A., & Prateek, J. (2020). Artificial Intelligence with Python. Packt Publishing Ltd.
Geron, A. (2019). Hands-on machine learning with Scikit-Learn, Keras, and TensorFlow: Concepts, tools, and techniques to build intelligent systems. O'Reilly Media.
Zheng, A., & Casari, A. (2018). Feature Engineering for Machine Learning principles and techniques for data scientists. O'Reilly Media, Inc.
https://sebastianraschka.com/faq/docs/dataprep-vs-dataengin.html
Raschka, S., & Mirjalili, V. (2019). Python Machine Learning: Machine Learning and Deep Learning with Python, scikit-learn, and TensorFlow 2 (Third). Packt Publishing Ltd.
Breiman, L. (1996). Bagging predictors. Machine Learning, 140, 123–140.
Breiman, L. (1999). Pasting small votes for classification in large databases and on-line. Machine learning, 36(1), 85-103.
https://scikit-learn.org/stable/modules/ensemble.html#bagging
Murphy, K. P. (2012). Machine learning: a probabilistic perspective. MIT press.
https://en.wikipedia.org/wiki/Bias%E2%80%93variance_tradeoff